Imputando Contexto Social a las encuestas

Autor/a

Aníbal Olivera

Fecha de publicación

8 de enero de 2025

1. Introducción

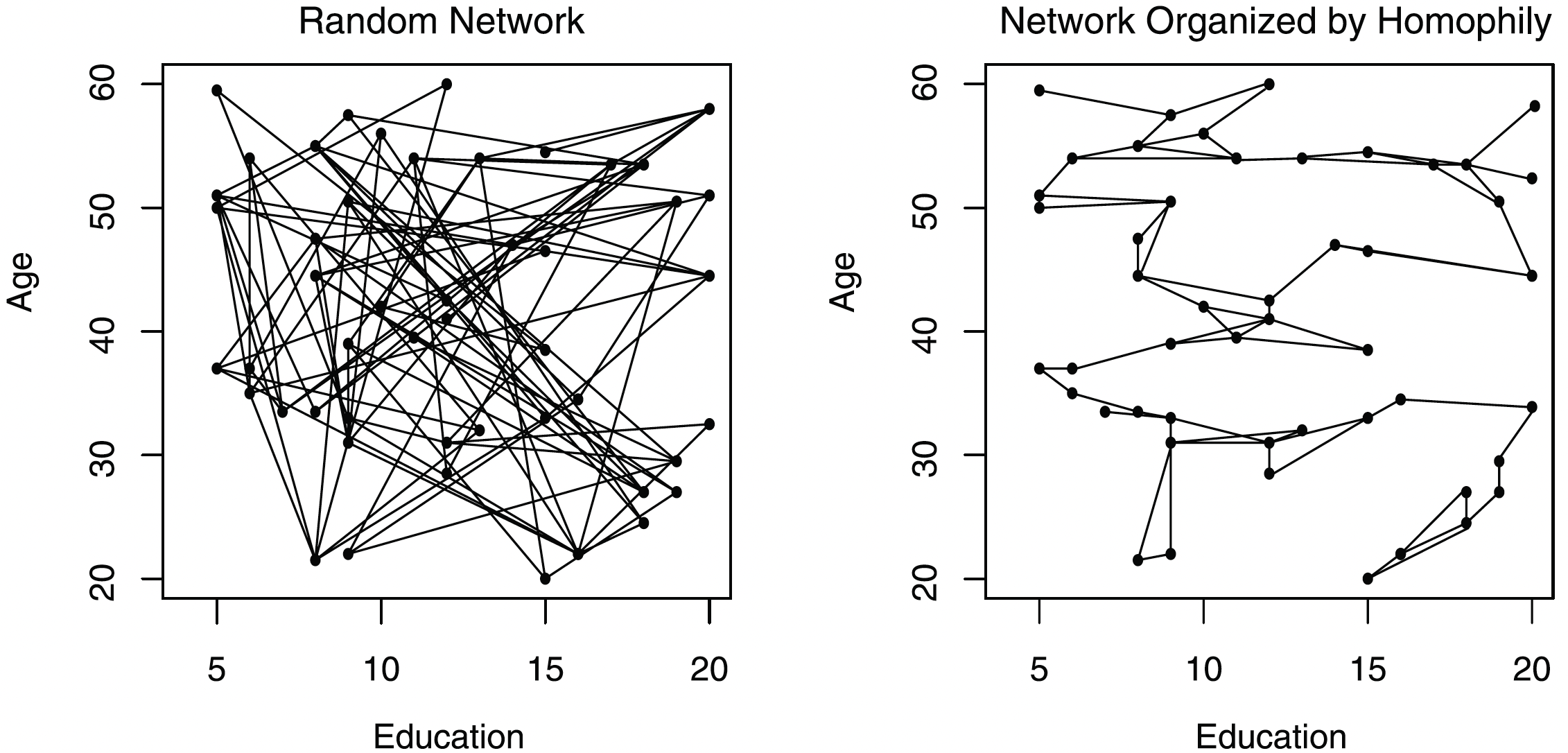
En la práctica es importante considerar los entornos sociales: conversaciones cotidianas, exposición repetida a puntos de vista, normas locales, etc. En otras palabras, dos individuos con demografías similares pueden diferir en sus actitudes si viven en “mundos sociales” distintos.

1.1 Los peligros de interpretar regresiones tradicionales

¿Qué pasa si los datos observados en una encuesta son el resultado de procesos de difusión en redes con homofilia ?

En el paper de DellaPosta et al. (2015) Why Do Liberals Drink Lattes? [https://doi.org/10.1086/681254] muestran que incluso sin ningún efecto causal directo de una variable sociodemográfica (ej. educación, ideología) sobre una conducta o preferencia (ej. consumo cultural), una regresión estándar puede producir coeficientes grandes y significativos, simplemente porque:

  • las personas interactúan principalmente con otros similares (homofilia), y
  • las conductas/actitudes se difunden a través de esas interacciones.

Supongamos que estimas el siguiente modelo: \[ y_i=\beta_0+\beta_1 \text { Educación }_i+\varepsilon_i \]

donde \(y_i\) es la actitud política, gusto cultural, consumo, etc. La interpretación puede ser que si \(\hat{\beta}_1>0\), se concluye que “la educación influye en la actitud \(y_i\).”

Ahora, DellaPosta et al. (2015) simulan un mundo donde:

  1. No hay efecto causal directo: \[ \text { Educación }_i \nrightarrow y_i \]

  2. La educación solo afecta con quién interactúas:

  • Alta educación → interactúas con gente similar.
  • Baja educación → lo mismo.

  1. Las actitudes se actualizan por influencia social: \[ y_i(t+1)=f\left(y_j(t): j \in N(i)\right) \]

  2. Como las redes son homofílicas:

  • Los altamente educados terminan compartiendo actitudes entre sí.
  • Lo mismo ocurre en otros grupos.

¿Qué observa el investigador ?

No ve la red ni la dinámica, solo una foto final:

  • Personas con alta educación \(\rightarrow\) valores similares de \(y\).

  • Personas con baja educación \(\rightarrow\) valores distintos.

Y cuando corre la regresión obtiene \(\hat{\beta}_1\) grande, y significativo.

Pero el supuesto implícito las observaciones son independientes condicionalmente a las covariables es falso porque \(y_i\) depende de \(y_j\): la regresión confunde un efecto individual, con un proceso relacional y contextual.

Pasos para imputar contexto social

Este módulo busca imputar contexto social en encuestas que no midieron redes personales. Para ello, se utiliza la metodología presentada en:

McPherson, M., & Smith, J. A. (2019). Network Effects in Blau Space: Imputing Social Context from Survey Data. Socius, 5. [10.1177/2378023119868591].

Figure 1. Example networks in two-dimensional Blau space.

  1. Estimar fuerza homofílica en una encuesta #1 que es representativa de una población con datos Ego-network: Al estimar \[ \operatorname{logit}\left(\operatorname{Pr}\left(Y_{i j}=1\right)\right)=\alpha+\boldsymbol{\beta}^{\top} \mathbf{d}_{i j}+\boldsymbol{\gamma}^{\top}\left(\mathbf{d}_{i j} \cdot \mathbb{I}_{2004}\right) \]

    obtenemos los coeficientes \(\hat{\boldsymbol{\beta}}, \hat{\boldsymbol{\gamma}}\), interpretados como “fuerza homofílica” por dimensión. (Nosotros usaremos \(\hat{\boldsymbol{\beta}_{\text{tot}}}=\hat{\boldsymbol{\beta}}+\hat{\boldsymbol{\gamma}}\)).

  2. Tomamos los coeficientes estimados en el paso 1 y los aplicamos a una encuesta focal #2 que es:

    • distinta de la encuesta de datos ego-network,
    • presenta un outcome \(y_i\) de interés,
    • que tiene las mismas covariables \(X_i\) (edad, educación, raza, religión, género, etc.) y
    • que es representativa de la misma población.

    Después de obtener los coeficientes, calculamos la probabilidad de interacción \(W_{ij}\) entre \(i\) y \(j\), basada en sus distancias sociales, así como los coeficientes del paso 1.

  3. Construimos el contexto social a ser imputado: \[ (W y)_i=\sum_{j=1}^{n} W_{ij}\,y_j. \] El término \((W y)_i\) es el promedio ponderado de \(y\) en los “alters imputados” de \(i\), ponderado por propensión homofílica a interactuar (cercanía en Blau space).

  4. Estimamos un modelo de autocorrelación espacial sobre la encuesta focal: \[ y = \rho (W y) + X \beta + \epsilon, \quad \epsilon \sim M V N\left(0, \sigma^2 I\right). \] donde \(\rho\) captura asociación entre outcome individual y el “clima” del entorno social imputado producido por \(W\).

1.2. Término Contextual

Los coeficientes \(\boldsymbol{\beta}\) (calculados usando case-control design) cuantifican cómo cambia la propensión al lazo al aumentar la distancia sociodemográfica:

\[ \text{logit}\big(\Pr(Y_{ij}=1)\big) = \alpha + \boldsymbol{\beta}^\top \mathbf{d}_{ij}. \]

Dado que el intercepto \(\alpha\) no es interpretable como densidad real bajo case-control, trabajamos con probabilidades relativas de lazo, definiendo un peso:

\[ w_{ij} \propto \exp\!\left(\boldsymbol{\beta}^\top \mathbf{d}_{ij}\right), \quad (\text{con } w_{ii} = 0), \]

que inducen una distribución sobre potenciales alters \(j\) que favorece pares cercanos en Blau space. A partir de esta estructura construimos una matriz de pesos \(W\) que representa “vecindad social” imputada (no geográfica), \[ W_{ij} = \frac{w_{ij} \cdot \mathbb{I}(j \in \mathcal{N}_i)}{\sum_{k \in \mathcal{N}_i} w_{ik}}. \]

donde \(\mathcal{N}_i \;=\; \{\, j \neq i \;:\; j \text{ está entre los } K \text{ mayores } w_{ij} \,\}\) es un término para seleccionar solo los vecinos más probables. Los valores en la matriz \(W\) reflejan los tipos de personas que \(i\) es probablemente conocer, dados las distancias sociales entre \(i\) y las demás personas en la población. Finalmente, calculamos el término contextual:

\[ (Wy)_i = \sum_{j \neq i} W_{ij}\, y_j, \]

donde \(y_j\) es la variable de interés del individuo \(j\). Intuitivamente, \((Wy)_i\) es una medida de “clima actitudinal” alrededor de \(i\).

2. Imputando Contexto Social (ANES 2016, Democrat Scale)

Para replicar el ejercicio empírico, utilizamos ANES 2016 (pre-election survey), que no tiene EGO-net. Imputaremos contexto social y evaluarémos si mejora la explicación de Democrat Scale (grado de simpatía/afinidad hacia el Partido Demócrata, reportado por McPherson & Smith) más allá de la demografía. Estimaremos dos modelos:

Modelo 1: (demografía) \[ y = X \beta + \epsilon, \quad \epsilon \sim \mathcal{N}(0, \sigma^2), \] donde \(\mathbf{x}_i\) incluye edad, educación, género, dummies de raza/etnicidad y religión.

Modelo 2: (demografía + contexto social imputado) \[ y = \rho (W y) + X \beta + \epsilon, \quad \epsilon \sim M V N\left(0, \sigma^2 I\right). \] donde \(\rho\) captura la asociación entre el outcome individual y el clima actitudinal del entorno social imputado.

El foco interpretativo será (i) si \(\rho>0\) y es estadísticamente distinguible de cero, y (ii) si la inclusión de \((Wy)_i\) reduce la magnitud de varios coeficientes demográficos, coherente con la lectura “contextual” discutida para Democrat Scale.

2.1. Construcción de Pesos (W)

Cargamos datos limpios de la ANES 2016 (preparados en anes-cleaning.qmd).

Código 
library(dplyr)
library(tidyr)
library(spdep)
library(spatialreg)
library(texreg)

# Cargar datos limpios
final_df <- readRDS("data/anes_2016_derived/anes_clean.rds")
cat("Datos ANES cargados. N =", nrow(final_df), "\n")
Datos ANES cargados. N = 4045

Construimos una matriz de pesos espaciales \(W\) basada en la similitud demográfica. Para eficiencia computacional, utilizamos una aproximación k-nearest (k=100) en probabilidad.

Código 
# Demográficos
vars_model <- c(
    "y", "age", "educ", "female", "race_raw", "relig_raw",
    "race_black", "race_hispanic", "race_asian", "race_native", "race_other",
    "relig_catholic", "relig_jewish", "relig_none", "relig_other"
)

final_df <- final_df %>%
    select(all_of(vars_model)) %>%
    drop_na()

X_age <- final_df$age
X_educ <- final_df$educ
X_sex <- final_df$female
X_race <- as.integer(final_df$race_raw)
X_relig <- as.integer(final_df$relig_raw)

# Calculamos distancias
D_age <- abs(outer(X_age, X_age, "-"))
D_educ <- abs(outer(X_educ, X_educ, "-"))
D_sex <- abs(outer(X_sex, X_sex, "-"))
D_race <- outer(X_race, X_race, function(x, y) ifelse(x != y, 1, 0))
D_relig <- outer(X_relig, X_relig, function(x, y) ifelse(x != y, 1, 0))

# Betas de Homofilia (Basados en Replicación V3 - GSS 2004)
# Estos valores corresponden a (beta + delta_2004) del modelo recreado
betas <- c(
    race = -1.352, relig = -1.354, sex = -0.256, age = -0.047, educ = -0.189
)

cat("Calculando distancias en Blau Space...\n")
Calculando distancias en Blau Space...
Código 
# 1. Calcular Distancias (Blau Space)
D_age <- abs(outer(X_age, X_age, "-"))
D_educ <- abs(outer(X_educ, X_educ, "-"))
D_sex <- abs(outer(X_sex, X_sex, "-"))
D_race <- outer(X_race, X_race, function(x, y) ifelse(x != y, 1, 0))
D_relig <- outer(X_relig, X_relig, function(x, y) ifelse(x != y, 1, 0))

# 2. Predictor Lineal (Log-odds)
eta <- betas["age"] * D_age + betas["educ"] * D_educ + betas["sex"] * D_sex +
    betas["race"] * D_race + betas["relig"] * D_relig

# 3. Pesos Crudos (Probabilidad relativa)
w_raw <- exp(eta)
diag(w_raw) <- 0

# 4. Selección Top-K (K=100) con PESOS (No Uniforme)
N <- nrow(final_df)
K <- 100
neighbors <- vector("list", N)
weights_list <- vector("list", N)

cat("Seleccionando Top-K vecinos y extrayendo pesos reales...\n")
Seleccionando Top-K vecinos y extrayendo pesos reales...
Código 
for (i in 1:N) {
    # Ordenar j por peso descendente (indices)
    row_w <- w_raw[i, ]
    ord <- order(row_w, decreasing = TRUE)
    candidates <- setdiff(ord, i)

    # Seleccionar Top K
    top_k_indices <- candidates[1:K]
    top_k_weights <- row_w[top_k_indices]

    # Ordenar índices para evitar error dgRMatrix en impacts()
    sort_idx <- order(top_k_indices)
    neighbors[[i]] <- top_k_indices[sort_idx]
    weights_list[[i]] <- top_k_weights[sort_idx]
}

class(neighbors) <- "nb"
attr(neighbors, "region.id") <- as.character(1:N)
attr(neighbors, "call") <- match.call()

# 5. Crear Objeto W (Normalizado por fila)
W_listw <- nb2listw(neighbors, glist = weights_list, style = "W", zero.policy = TRUE)

cat("Matriz W construida.\n")
Matriz W construida.

2.2. Modelos de Regresión

Estimamos dos modelos para explicar la simpatía por el Partido Demócrata (\(Y\)):

  1. Modelo 1 (Base): Solo predictores demográficos (\(X\)).

\[ y = X \beta + \epsilon, \quad \epsilon \sim \mathcal{N}(0, \sigma^2). \]

  1. Modelo 2 (Contexto): Modelo de autocorrelación espacial (SAR/Spatial Lag).

\[ y = \rho (W y) + X \beta + \epsilon, \quad \epsilon \sim M V N\left(0, \sigma^2 I\right). \]

Código 
library(stargazer)

# Fórmula Base
fmla_base <- y ~ age + educ + female +
    race_black + race_hispanic + race_asian + race_native + race_other +
    relig_catholic + relig_jewish + relig_none + relig_other

# Modelo 1: OLS
m1 <- lm(fmla_base, data = final_df)

# Modelo 2: SAR (Spatial Autoregressive)
m2_sar <- spatialreg::lagsarlm(
    formula     = fmla_base,
    data        = final_df,
    listw       = W_listw,
    method      = "eigen",
    zero.policy = TRUE,
    na.action   = na.fail
)

# Resultados con texreg (htmlreg)
htmlreg(list(m1, m2_sar),
    custom.model.names = c("Base (OLS)", "Contextual (SAR)"),
    caption = "Democrat Scale (ANES 2016) - OLS vs SAR",
    # Mapeo de coeficientes para visualización limpia
    custom.coef.map = list(
        "(Intercept)" = "Intercept",
        "age" = "Age",
        "educ" = "Education",
        "female" = "Female",
        "race_black" = "Black",
        "race_hispanic" = "Hispanic",
        "race_asian" = "Asian",
        "race_native" = "Native American",
        "race_other" = "Other race",
        "relig_catholic" = "Catholic",
        "relig_jewish" = "Jewish",
        "relig_none" = "None",
        "relig_other" = "Other religion",
        "rho" = "Spatial parameter"
    ),
    center = TRUE,
    doctype = FALSE,
    include.rsquared = TRUE, include.adjrs = FALSE, include.nobs = TRUE,
    include.rmse = FALSE, se = FALSE
)
Democrat Scale (ANES 2016) - OLS vs SAR
  Base (OLS) Contextual (SAR)
Intercept 35.74*** 16.93***
  (1.81) (3.15)
Age -0.01 0.01
  (0.03) (0.03)
Education 0.02 0.03
  (0.06) (0.06)
Female 6.59*** 5.43***
  (0.88) (0.89)
Black 32.64*** 18.99***
  (1.54) (2.37)
Hispanic 16.22*** 9.38***
  (1.51) (1.80)
Asian 10.05*** 6.25*
  (2.47) (2.49)
Native American 14.08* 10.97
  (5.98) (5.94)
Other race 7.89*** 4.97*
  (2.27) (2.28)
Catholic 5.81*** 3.07*
  (1.24) (1.27)
Jewish 16.29*** 10.11**
  (3.24) (3.26)
None 10.00*** 4.85***
  (1.26) (1.32)
Other religion -0.36 -0.31
  (1.23) (1.22)
Spatial parameter   0.48***
    (0.07)
R2 0.14  
Num. obs. 4045 4045
Parameters   15
Log Likelihood   -19173.95
AIC (Linear model)   38426.85
AIC (Spatial model)   38377.90
LR test: statistic   50.95
LR test: p-value   0.00
***p < 0.001; **p < 0.01; *p < 0.05

2.3. Discusión de Resultados


--- Comparación Simplificada de Coeficientes ---
Variable Beta OLS Beta SAR % Reducción
race_black Black 32.64 18.99 41.84
race_hispanic Hispanic 16.22 9.38 42.18
relig_catholic Catholic 5.81 3.07 47.21
female Female 6.59 5.43 17.50

Parte de lo que uno atribuiría a “efectos individuales” de raza, religión, educación, etc., en realidad refleja que distintos grupos tienden a habitar contextos sociales distintos.

  • Término \(\rho\) positivo y estadísticamente significativo: quienes están, en promedio, rodeados por alters que muestran mayor simpatía por los demócratas tienden también a reportar mayor simpatía.

  • Religión: el contraste entre católicos vs. protestantes ya no es estadísticamente significativo al controlar contexto.

  • Raza: los efectos son menores, y el contraste entre white/asian y white/native es menos significativo.

¿Cuánto importa el contexto?

Para ilustrar la magnitud del efecto contextual, compararemos el cambio predicho comparando a una misma persona en dos contextos diferentes, y contrastaremos ese cambio con efectos puramente demográficos.

Código 
# 1. Obtener coeficientes del Modelo 2 (Contextual)
coefs <- coef(m2_sar)

# --- Efecto Contextual (Simulación aproximada) ---
# En SAR: Efecto global de cambiar Wy es complejo.
# Aproximación simple usando el Rho estimado y la distribución observada de Wy (lag)
Wy_pred <- lag.listw(W_listw, final_df$y) # Wy imputado ex-post
rho_est <- m2_sar$rho

# Comparamos moverse del percentil 10 al 90 de ese `Wy` latente
Wy_p10 <- quantile(Wy_pred, 0.10, na.rm = TRUE)
Wy_p90 <- quantile(Wy_pred, 0.90, na.rm = TRUE)
delta_context <- rho_est * (Wy_p90 - Wy_p10)

cat(sprintf("CONTEXT EFFECT (P10 -> P90 Wy): +%.2f puntos\n", delta_context))
CONTEXT EFFECT (P10 -> P90 Wy): +14.24 puntos
Código 
# --- Efecto Demográfico --- (Race: White -> Black)
delta_race_black <- coefs["race_black"]
cat(sprintf("RACE EFFECT (White -> Black):  +%.2f puntos\n", delta_race_black))
RACE EFFECT (White -> Black):  +18.99 puntos
Código 
# --- Efecto Demográfico --- (Sex: Male -> Female)
delta_female <- coefs["female"]
cat(sprintf("SEX EFFECT (Male -> Female):   +%.2f puntos\n", delta_female))
SEX EFFECT (Male -> Female):   +5.43 puntos

En un modelo SAR, los coeficientes solo miden el impacto inmediato (directo). Pero el término \(\rho (Wy)\) genera un feedback: el cambio en \(i\) afecta a sus vecinos, quienes a su vez re-afectan a \(i\). Los “Impactos Totales” capturan la suma de estos efectos directos + indirectos (spillover).

Código 
# 2. Impactos (Efectos Totales)
set.seed(123)
imp <- spatialreg::impacts(m2_sar, listw = W_listw, R = 200)

# Mostramos solo el resumen de efectos Totales para variables clave
imp_summary <- summary(imp, zstats = TRUE, short = TRUE)

# Extraer y combinar solo Estimaciones y P-values para una visualización limpia
mat_impacts <- imp_summary$res$total
mat_pvals <- imp_summary$pzmat

# Generamos una tabla con los resultados
df_impacts_print <- data.frame(
    Directo = imp_summary$res$direct,
    Indirecto = imp_summary$res$indirect,
    Total = imp_summary$res$total,
    p_Total = imp_summary$pzmat[, "Total"]
)

# Impactos Promedio (con p-valor para Efecto Total):
cat("\n**Impactos Promedio (con p-valor para Efecto Total):**\n")

Impactos Promedio (con p-valor para Efecto Total):

Código 
print(knitr::kable(df_impacts_print, digits = 4))
Directo Indirecto Total p_Total
age dy/dx 0.0083 0.0076 0.0159 0.7040
educ dy/dx 0.0291 0.0268 0.0559 0.5921
female dy/dx 5.4530 5.0232 10.4762 0.0000
race_black dy/dx 19.0495 17.5480 36.5975 0.0000
race_hispanic dy/dx 9.4103 8.6685 18.0788 0.0000
race_asian dy/dx 6.2659 5.7720 12.0380 0.0122
race_native dy/dx 11.0072 10.1396 21.1468 0.0677
race_other dy/dx 4.9900 4.5967 9.5868 0.0409
relig_catholic dy/dx 3.0779 2.8353 5.9131 0.0053
relig_jewish dy/dx 10.1413 9.3420 19.4833 0.0029
relig_none dy/dx 4.8619 4.4787 9.3406 0.0002
relig_other dy/dx -0.3093 -0.2849 -0.5942 0.7883
Código 
cat("\n**Comparación: Beta OLS vs Impacto Total SAR**\n")

Comparación: Beta OLS vs Impacto Total SAR

Código 
# Recuperamos coeficientes OLS (m1)
c_ols <- coef(m1)

# Variables clave a comparar (nombres en OLS / Modelo)
vars_comp_ols <- c("race_black", "race_hispanic", "relig_catholic", "female")

# Extraer vector de totales
vec_total <- as.vector(imp_summary$res$total)

# Obtener nombres de variables del modelo SAR (excluyendo Intercept y Rho)
names_sar_model <- names(coef(m2_sar))
names_clean <- names_sar_model[!names_sar_model %in% c("(Intercept)", "rho", "lambda")]

# Asegurar que longitudes coincidan antes de asignar (seguridad)
if (length(vec_total) == length(names_clean)) {
    names(vec_total) <- names_clean
} else {
    warning("Longitud de impactos y variables no coincide. Revisar nombres.")
}

# Nombres para mostrar en tabla
names_display <- c("Black", "Hispanic", "Catholic", "Female")

# Construir tabla
df_compare_total <- data.frame(
    Variable = names_display,
    Beta_OLS = c_ols[vars_comp_ols],
    SAR_Total = vec_total[vars_comp_ols]
)

# Calcular diferencia y reducción
df_compare_total$Diff_Abs <- df_compare_total$Beta_OLS - df_compare_total$SAR_Total
df_compare_total$Pct_Reduction <- (df_compare_total$Diff_Abs / df_compare_total$Beta_OLS) * 100

# Mostrar tabla final
print(knitr::kable(df_compare_total,
    digits = 2,
    row.names = FALSE,
    col.names = c("Variable", "Beta OLS", "SAR Total Impact", "Diff", "% Reducción")
))
Variable Beta OLS SAR Total Impact Diff % Reducción
Black 32.64 36.60 -3.95 -12.11
Hispanic 16.22 18.08 -1.86 -11.45
Catholic 5.81 5.91 -0.10 -1.76
Female 6.59 10.48 -3.89 -59.03

3. Interludio: Simulación de Redes Completas

Si bien la imputación en Blau Space nos permite calcular un \((Wy)\) para cada individuo, no produce una red explícita de “quién es amigo de quién” a nivel global.

Para generar una topología de red completa que respete los principios de homofilia estimados, utilizamos un Exponential Random Graph Model (ERGM), que nos permite simular grafos donde la probabilidad de un lazo depende de:

  1. Homofilia paramétrica: exactamente los mismos coeficientes (\(\boldsymbol{\beta}\)) de la Sección 2.1.

  2. Densidad (Edges): nos dice cuántos lazos existen en total, así que ajustamos el parámetro edges (intercepto) hasta alcanzar la densidad observada en redes reales.

Fijaremos una densidad de 0.03 (aprox. 30 lazos por cada 200 pares posibles).

3.1. Calibración edges

Usaremos una sub-muestra de N=200 individuos para agilizar la simulación computacional. Utilizaremos un proceso iterativo para encontrar el intercepto que produce la densidad deseada.

Código 
library(ergm)
library(network)

# 1. Submuestreo (N=200)
set.seed(123)
target_n <- 200
idx_sample <- sample(nrow(final_df), target_n)
small_df <- final_df[idx_sample, ]

# 2. Inicializar Red Vacía con Atributos
net <- network(target_n, directed = FALSE, density = 0)
set.vertex.attribute(net, "race", as.character(small_df$race_raw))
set.vertex.attribute(net, "sex", as.character(small_df$female)) # 0/1
set.vertex.attribute(net, "edu_num", small_df$educ)
set.vertex.attribute(net, "age", small_df$age)
set.vertex.attribute(net, "relig", as.character(small_df$relig_raw))

# 3. Definir Coeficientes (Mismos valores Sección 2.1)
# IMPORTANTE: ERGM usa 'nodematch' (coincidencia), por lo que invertimos el signo
# de los coeficientes de 'diferencia' para raza, sexo y religión.
# Las variables continuas (edad, educ) usan 'absdiff', manteniendo su signo negativo.
coefs_target <- c(
    edges = -6.5, # Valor inicial ("semilla")
    nodematch.race = 1.352, # -(-1.352)
    nodematch.sex = 0.256, # -(-0.256)
    nodematch.relig = 1.354, # -(-1.354)
    absdiff.age = -0.047,
    absdiff.edu_num = -0.189
)

# Fórmula del Modelo
ergm_formula <- net ~ edges + nodematch("race") + nodematch("sex") +
    nodematch("relig") + absdiff("age") + absdiff("edu_num")

# 4. Calibración Rápida de Densidad (Max 5 Iteraciones)
target_density <- 0.03
current_edges <- -4.0 # Ajustamos el intercepto inicial para densidad más alta
step_size <- 0.5

cat("Calibrando parámetro 'edges' para densidad ~0.03...\n")
Calibrando parámetro 'edges' para densidad ~0.03...
Código 
for (i in 1:5) {
    coefs_target["edges"] <- current_edges

    # Simular 1 red
    sim_net <- simulate(ergm_formula, coef = coefs_target, verbose = FALSE)
    current_density <- network.density(sim_net)

    cat(sprintf("Iter %d: Edges Coef = %.2f -> Densidad = %.5f\n", i, current_edges, current_density))

    # Ajuste simple de búsqueda
    if (current_density < target_density) {
        current_edges <- current_edges + step_size # Subir probabilidad
    } else {
        current_edges <- current_edges - step_size # Bajar probabilidad
    }
    # Reducimos paso para refinar
    step_size <- step_size * 0.6
}
Iter 1: Edges Coef = -4.00 -> Densidad = 0.02307
Iter 2: Edges Coef = -3.50 -> Densidad = 0.03784
Iter 3: Edges Coef = -3.80 -> Densidad = 0.02935
Iter 4: Edges Coef = -3.62 -> Densidad = 0.03322
Iter 5: Edges Coef = -3.73 -> Densidad = 0.03000

3.2. Visualización de red simulada

Genial, ahora que tenemos los coeficientes calibrados, podemos generar la red final.

Código 
final_net <- simulate(ergm_formula, coef = coefs_target, seed = 111, verbose = FALSE)
cat("Densidad Final:", network.density(final_net), "\n")
Densidad Final: 0.02854271

Finalmente, visualizamos la red resultante. Los nodos están coloreados por raza, mostrando cómo la homofilia genera agrupamientos (“clusters”) naturales en la red social sintética.

Código 
library(igraph)
library(intergraph)

# 1. Convertir a igraph
g_sim <- asIgraph(final_net)

# 2. Extraer Componente Gigante
comps <- decompose(g_sim, mode = "weak")
g_main <- comps[[which.max(sapply(comps, vcount))]]

# Colores por Raza (en el componente)
V(g_main)$color <- case_when(
    V(g_main)$race == "1" ~ "lightblue", # White
    V(g_main)$race == "2" ~ "tomato", # Black
    V(g_main)$race == "3" ~ "gold", # Hispanic
    TRUE ~ "gray"
)

# Layout: Dividimos el espacio gráfico
par(mfrow = c(2, 1), mar = c(4, 4, 2, 1))

# --- Plot 1: Red (Giant Component) ---
plot(g_main,
    layout = layout_with_fr(g_main),
    vertex.size = 5,
    vertex.label = NA,
    edge.color = adjustcolor("black", alpha.f = 0.3),
    main = paste("Simulación ERGM (Componente Principal), N=", vcount(g_main))
)
legend("topleft",
    legend = c("White", "Black", "Hispanic"),
    col = c("lightblue", "tomato", "gold"), pch = 19, bty = "n", cex = 0.8
)

# --- Plot 2: Distribución de Grados ---
deg <- degree(g_sim)
mean_deg <- mean(deg)

hist(deg,
    breaks = 15, col = "steelblue", border = "white",
    main = "Distribución de Grados",
    xlab = "Grado (Número de conexiones)", ylab = "Frecuencia"
)
abline(v = mean_deg, col = "red", lwd = 2, lty = 2)
text(mean_deg, max(table(deg)) * 0.9,
    paste("Media:", round(mean_deg, 1)),
    pos = 4, col = "red", cex = 0.9
)

Red simulada (N=200): Componente Principal y Distribución de Grado